Előszó

Új rovatot indítok ezeken az oldalakon azzal a szándékkal, hogy bemutassam látogatóimnak a számítógépes grafika eme tájékát. 1985-ben kezdtem megismerkedni a fraktálok világával a Scientific American 1985/2 számából, amely azóta is bűvöletében tart. A korabeli számot "WEB-es" köntösbe bújtatva  adom közzé, bízva abban hogy másokat is érdekel a matematika e látványos gyönyörűsége..

ÉSZJÁTÉK

A számítógép mint mikroszkóp behatolhat a matematika legbonyolultabb területeire
Írta: A. K. Dewney

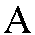Mandelbrot-halmaz csendes bonyolultságban tölti ki a komplex síknak nevezett óriási kétdimenziós számsík közepét. Ha a számokon bizonyos műveleteket többször egymás után elvégzünk, a halmazhoz nem tartozó számok a végtelenbe menekülnek. A halmazon belüli számok lassan körbevonulnak vagy körbetáncolnak. A határ közelében aprólékosan koreografált vándorlás jelzi az instabilitás támadását. A részletek végtelen visszatérése változatosságával, bonyolultságával és különös szépségével ámulatba ejtő.
   A halmazt Benoit B. Mandelbrotról, az IBM Thomas J. Watson Kutatóközpontjának (Yorktown
Heights, N.Y.) kutató munkatársáról nevezték el.   Geometriai alakzatokkal  folytatott munkája során Mandelbrot kifejlesztette az általa a törtek  geometriájának nevezett szakterületet, a tört  dimenziójú  alakzatok, a fraktálok tanulmányozását.  A Mandelbrothalmaz határa  főként törtes, de annál egyszersmind sokkal több is.
   Egy viszonylag egyszerű program segítségével a számítógép egyfajta mikroszkóppá alakítható, amellyel a Mandelbrothalmaz határát szemügyre vehetjük. Elvben bármely része felől közelíthetünk a halmazhoz, hogy közelebbi, tetszőleges nagyítású képet nyerjünk. Távolról szemlélve a halmaz zömök, szemölccsel borított, fekvő nyolcashoz hasonlít. Az alakzat belseje baljóslatúan fekete. Ezt az alakzatot éles fehér fényudvar övezi, amely a sík külső övezeteinek mély kékjeivé és feketéivé alakul át.
  A Mandelbrot-halmazhoz közelítve azt tapasztaljuk, hogy mindegyik szemölcs egy apró, az anyahalmazhoz hasonló formájú alakzat. Az egyik apró alakzathoz még jobban közelítve azonban egészen más minta tárul elénk: szervesnek látszó indák és kacsok tobzódnak előttünk spirálisan és sorokba rendeződve. Egy indát kinagyítva ismét más színtér válik láthatóvá: az inda spirális párokból áll, s finom hidacskák kapcsolódnak hozzá. A hidacskák egyikét kinagyítva kiderült, hogy két indája van, amelyek középről ágaznak szét. Ennek a középnek a közepén négysávos híd van további négy indával, s ezeknek az indáknak a közepén a Mandelbrot-halmaz másik változatát találjuk.
  A kinagyított változat nem egészen ugyanaz a Mandelbrot-halmaz. Ahogy mint egy zoom-objektívval folytatjuk a közelítést, hasonló elemek látszanak feltűnni, azonban közelebbről szemügyre véve őket, mindig kiderülnek a különbségek. Ilymódon előre haladva a dolgok végtelenül változatosak és félelmetesen pompásak.
  Az alábbiakban két számítógépprogramot mutatok be. Mindkettő az olyan iterációs műveletek hatásait tárja fel, amelyek végül a Mandelbrot-halmazhoz vezetnek. Az e havi "Észjáték" hasábjainak színes illusztrációit az első program állította elő. A program olyan személyi számítógépeken történő futtatáshoz is adaptálható, amelyek grafika előállítására alkalmas hardver- és szoftverelemekkel rendelkeznek. Ez a program kielégítő képet készít akkor is, ha valaki csak fekete-fehér monitorhoz jut hozzá. A második program azoknak az olvasóknak való, akiknek hozzám hasonlóan szükségük van időnként a végtelen komplexitása helyett a véges kézzelfogható egyszerűségére.

ét értelme van itt most a "komplex" szónak. Az általános jelentés nyilvánvalóan a Mandelbrot-halmaz jelzőjének felel meg, van azonban ennek a szónak egy második, inkább szakmai jelentése is. Egy szám akkor komplex, ha két - történeti okokból valósnak és képzetesnek nevezett-részből áll. Ezeknek a kifejezéseknek a továbbiakban nincs semmiféle fontosságuk: a komplex szám két részét nevezhetjük akár Incinek és Fincinek is. Így például a 7+4i komplex szám, melynek valós része 7 (Inci) és képzetes része 4i (Finci). A négyes számot követő dőlt i betű jelzi, hogy a komplex számnak melyik része képzetes.
  A síkban minden komplex szám egy ponttal ábrázolható: a komplex számok síkját komplex síknak nevezzük. Ahhoz, hogy a 7+4i helyét a komplex síkban megtaláljuk, kezdjük a munkát a 0 komplex számmal, vagyis 0+0i-vel. Most mérjünk fel hét egységet keletre, majd négy egységet északra.
Az eredményül kapott pont ábrázolja a 7+4i komplex számot.
A komplex sík az ilyen számok megszámlálhatatlan végtelenjéből áll. A komplex számoknak mind a valós, mind a képzetes része pozitív vagy negatív, egész vagy tizedestört is lehet.
  Két komplex szám összeadása vagy szorzása egyszerű. A 3-2i és a 7+4i komplex számok összeadásánál a részeket különkülön kell összegezni; az összeg 10+2i lesz. A komplex számok szorzása csak kissé bonyolultabb. Ha az i szimbólumot úgy kezeljük például, mint a középiskolai algebrában az x-et, a 3-2i és a 7+4i szorzatának eredménye 21+12i-14i-8i² lesz. Ennél a pontnál az i szimbólumnak egy különleges tulajdonságát kell bevonni a játékba: i*i egyenlő -1-gyel. Így az eredményt a valós és képzetes részek öszszevonásával a következő alakra egyszerűsíthetjük: azaz 29-2i.
  Most már le lehet írni azt az iteratív eljárást, amely a Mandelbrot-halmazt előállitja. Kezdjük a z²+c algebrai kifejezéssel, ahol z komplex változó, c pedig egy bizonyos állandó komplex szám. Kezdetben z értéke legyen egyenlő a 0 komplex számmal. Ezek után a z négyzete is 0, és a z², valamint a c összeadásakor kapott eredmény éppen c lesz. Helyettesítsük be ezt a kapott eredményt z helyére a z²+c kifejezésben! Az új összeg c²+c. Ezt az eredményt helyettesítsük be újra a z helyére. A következő összeg (c²+c)²+c² lesz. Folytassuk tovább ezt az eljárást úgy, hogy az utolsó lépés eredménye legyen a következő lépés kiindulása.
    Különös dolgok történnek, amikor az iterációt c egyes értékeire elvégezzük. Ha például c = 1+i:
                       első iteráció: 1+3i
                       második iteráció: -7+7i
                       harmadik iteráció: 1-97i
   Figyeljük meg, hogy a valós és a képzetes rész növekedhet, csökkenhet és előjelét is változtathatja. Ha ez az iterációs folyamat folytatódik, az eredményül. kapott komplex számok fokozatosan egyre nagyobbak lesznek.
  Mit is értünk vajon egy komplex szám nagyságán? Minthogy a komplex számok a sík pontjainak felelnek meg, a távolság fogalma megfelelőnek látszik. Egy komplex szám nagysága a szóban forgó szám 0 ponttól mért távolságával egyenlő. Ez a távolság egy olyan derékszögű háromszög átfogója, melynek két befogója a komplex szám valós és képzetes része. Ennél fogva a szám nagyságának meghatározásához emeljük négyzetre a komplex szám részeit, adjuk össze a két négyzetet, majd vonjunk gyököt az összegből. A 7+4i komplex szám nagysága például a 7²+4² összeg négyzetgyöke, vagyis körülbelül 8,062. A komplex számok az imént leírt iterációs folyamat során egy bizonyos értéket elérve nagyon gyorsan növekednek: néhány további iteráció után ezek a számok meghaladják bármely számítógép kapacitását.
Szerencsére figyelmen kívül hagyhatom a fékevesztett növekedést eredményező c komplex számokat. A Mandelbrot-halmaz azoknak a c komplex számoknak a halmaza, amelyekre z²+c nagysága bármilyen nagyszámú iteráció elvégzése után is véges. Az itt bemutatott program ezeket a számokat keresi meg. Ebben a munkában nyújtott segítségéért lekötelezettje vagyok John H. Hubbardnek, a Cornell Egyetem matematikusának. Hubbard szaktekintély a Mandelbrot-halmaz terén, s az elsők között volt, akik számítógép segítségével generált képet készítettek róla. E cikk képeinek többségét Heinz-Otto Peitgen és munkatársai készítették a Brémai Egyetemen. Peitgen Hubbardtól tanulta művészetét.

ubbard programja ihlette azt a programot, amelyet MANDELZOOMnak neveztek el. E program létrehoz egy pic (kép) nevű tömböt, amelyre a képek megőrzéséhez lesz szükség. A pic tömbbe az egyes képelemek, úgynevezett pixelek kerülnek, rácsszerű elrendezésben. Hubbard tömbjének 400 oszlopa és 400 sora van, Peitgené még ennél is nagyobb. Azoknak az olvasóknak, aki személyes használatukra kívánják adaptálni a MANDELZOOM programot, felszerelésükhöz és alkatukhoz illő tömböt kell választaniuk. A nagyobb tömböknél a képre hosszabban kell várni, viszont jobb a kép felbontása.
  A MANDELZOOM első részében a vizsgálathoz ki kell választani a komplex sík egy négyzetes területét. A négyzet délnyugati sarkát azzal a komplex számmal határozzuk meg, amely ennek a pontnak felel meg. A programban két változó - az acorner asarok) és a bcorner (bsarok) - teszi lehetővé, hogy a komplex szám valós és képzetes részét egyenként megadjuk. A négyzet oldalainak hosszúságát a side (oldal) változó értékének megadásával határozzuk meg.
  A program második része a gap (hézag) változó nagyságának kiszámításával állítja be a pic tömböt úgy, hogy az a kérdéses négyzethez illeszkedjék. Agap változó jelöli a négyzeten belül a szomszédos képelemek közötti távolságot. Ahhoz, hogy a gapet megkapjuk, osszuk el a side-ot a pic sorainak (vagy oszlopainak) számával.
  A program lelke a harmadik rész. A Mandelbrot sorozatban itt keressük ki a c komplex számokat és olyan számokhoz rendelünk bizonyos színeket, amelyek valamilyen értelemben közel vannak egymáshoz. Az eljárást egyszer minden képelemre végre kell hajtani; így Hubbard 400x400-as tömbjéhez 160000 külön számításra van szükség. Tételezzük fel, hogy a program éppen az m-ik sorban és az n-ik oszlopban lévő képelemen dolgozik; harmadik része ekkor négy lépésre bomlik.
  1. Kiszámít egy c komplex számot, amelyről feltételezzük, hogy a képelemet ábrázolja: az nxgap szorzatot hozzáadja az acorner-hez és megkapja a c komplex szám bc képzetes részét. Az i képzetes számot nem szükséges beépíteni a programba.
  2. Induláskor állítsunk be egy z komplex változót (melynek részei az és bz) úgy, hogy legyen egyenlő a 0+Oi komplex számmal. Állítsunk be egy count (számláló) nevű egész értékű változöt 0 értékre.
  3. Ismételten hajtsuk végre a következő három lépést mindaddig, amíg z nagysága meghaladja a 2-t, vagy pedig a count nagysága túllépi az 1000-es értéket, attól függően, hogy melyik következik be először:
                           z <-- z²+c
                           count <-- count+1
                           nagyság <--z nagysága
Vajon miért olyan fontos a 2-es szám? A komplex számok iterációja elméletének egyszerű eredménye garantálja, hogy az iteráció a z szám értékét akkor, és csak akkor növeli végtelenre, ha valamelyik lépésben z vagy eléri a 2-t, vagy annál nagyobb értéket vesz fel. Kiderül, hogy alig néhány iteráció elvégzése után viszonylag sok pont értéke éri el a 2-t, s helye ezzel a végtelenbe kerül. Lassúbb rokonaik a count-változó nagyobb értékeinél egyre ritkábban fordulnak elő.
  4. Rendeljünk egy színt a pic(m,n) ponthoz annak megfelelően, hogy a 3. lépésben az a count változó milyen értéket ért el. Jelenítsük meg e~h a színt a megfelelő képelemnél a képernyőn. Jegyezzük meg, hogy egy képelem színe az apró területen belül csak egyetlen komplex szám függvénye, nevezetesen azé, amelyik a terület északkeleti sarkán van; ezért ennek a számnak a viselkedése képviseli a teljes képelem viselkedését.
A színösszeállításnál szükség van arra, hogy a tömbön belül előforduló count értékek tartományát színenként altartományokra csoportosítsuk. Azon képelemeknek a színe, amelyeknél a z nagysága néhány iteráció után eléri a 2-t, legyen vörös. Azoknál a képelemeknél, ahol z értéke csak viszonylag sok iteráció után éri el a 2-t, válasszuk a színkép másik végéről a lilát. Azokról a képelemekről, amelyeknél a z értéke még 1000 iteráció elvégzése után is kisebb mint 2, feltételezzük, hogy a Mandelbrot-halmazon belül vannak; ezek feketék.
Okosan tesszük, ha a színeket az illető négyzetre vonatkozó count változó tartományának meghatározásáig nem írjuk elő. Ha ez a tartomány szűk, akkor a teljes színskála ehhez rendelhető. Ezért Hubbard azt ajánlja, hogy a 4. lépésben csak a count értékét rögzítsük a pic tömb egyes elemeire. Ezután külön program tapogathatja le a tömböt, hogy a count kis és nagy értékeit meghatározza, és a színskálát ennek megfelelően feloszthassa. Azok az olvasók, akik idáig eljutottak, bizonyára találnak működőképes megoldást.

színes monitorral nem rendelkező olvasók fekete-fehérrel is dolgozhatnak. Az r iteráció elvégzése után 2-nél nagyobb z komplex számok fehérek lesznek, a többi fekete, r értéke ízlés szerinti. Nehogy a program egész éjszaka fusson, legyen a tömb mondjuk 100 soros és 100 oszlopos. Hubbard szerint a pontonként maximálisan elvégzett iterációk számának ezerről százra való csökkentése is indokolt. Egy ilyen program végterméke a lap alján látható szuggesztív, "pointilista" kép. Ilyen teljesítményre képes vajon egy személyi számítógép "gumiobjektívje"? Ez bizonyos mértékben attól függ, hogy a gép mekkora számokkal képes dolgozni. Magi szerint (aki számítógépes mindenesem a Western Ontario Egyetemen) például az IBM PC a 8088-as mikroprocesszort használja. Ezt a chipet az Intel Corporation gyártja, 16 bites számok kezelésére tervezték: a kettős pontosságnak nevezett lehetőséggel a számok hosszúsága 32 bitre növelhető. Magivel kiszámítottuk, hogy e kettős pontossággal körülbelül 100000-szeres nagyítás valósítható meg. Nagyobb pontosságú szoftver, amely ezeket a számokat össze tudja fűzni, a numerikus pontosságot értékes jegyek százaira is képes fokozni. Ezzel a pontossággal a Mandelbrot-halmaznak elvileg elérhető nagyítása sokkal nagyobb, mint az a nagyítás, amire egy atommag láthatóvá tételéhez van szükség.
Hol kell a komplex síkot átkutatnunk? Természetesen a Mandelbrot-halmaz közelében, de pontosan hol? Hubbard azt mondja, hogy "arrafelé gyönyörű tájak milliárdjai vannak". Mint a végtelen szépségű vidéket járó turista, Hubbard eláraszt ajánlatokkal a felderítésre váró helyekkel kapcsolatban. Persze ezeket a tájakat nem Hong Kongnak vagy Kis-Antilláknak hívják, hanem így: "Próbáld ki a valós rész 0,26 és 0,27, valamint a képzetes rész 0 és 0,01 közötti területét." Hubbard két másik vidéket is javasol:
               Valós rész                     Képzetes rész  
            -0,76 - -0,74                   0,01-0,03
            -1,26 - -1,24                   0,01-0,03
Az az olvasó, aki a cikkünket kísérő színes képeket nézi, emlékezetében kell tartsa, hogy a nem fekete színű pontok nem- tartoznak a Mandelbrot-halmazhoz. A szépség nagy része a kiszökő pontokhoz rendelt színek kavalkádjában található. Valóban, ha valaki csak a halmazt magát nézné, annak a képe nem lenne ily szép: teljes egészében rostok, és saját miniatűr változatai borítják.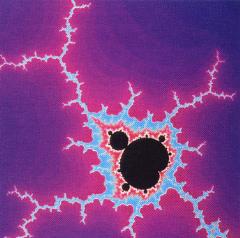Ténylegesen egyik miniatűr Mandelbrot sem pontos másolata az anyahalmaznak, és egyik sem pontosan ugyanolyan, mint a másik. Az anyahalmaz közelében még további miniatűr Mandelbrotok helyezkednek el, melyek látszólag szabadon lebegnek a komplex síkon. Megjelenésük megtévesztő. Hubbard és munkatársai meghökkentő elméleti tételt bizonyítottak. Adrian Douady (Párizsi Egyetem) megállapítja, hogy a Mandelbrot-halmaz összefüggő. Ennélfogva a síkban lebegni látszó miniatűr Mandelbrotok is rostokkal csatlakoznak az anyahalmazhoz. A miniatúrák az anyahalmaz közelében csaknem bárhol megtalálhatók, és csaknem minden méretben előfordulnak. A terület minden négyzetében végtelen számú miniatúra van, többnyire azonban csak néhányat láthatunk közülük bármely adott nagyítás mellett. Hubbard szerint a Mandelbrot-halmaz "a matematika legbonyolultabb képződménye."
Azok az olvasók, akik érdeklődnek a Mandelbrot-halmaz további színes képei iránt, s akiket foglalkoztatnak a matematika más területei is, írásban kérhetik Hubbardtől (Department of Mathematics, Cornell University, Ithaca, N. Y. 14853) a témáról szóló könyvecskét.

végtelenek bonyolultságába belefáradva jóleső menedéket találunk a véges birodalmában. A valós egész számok véges sorozatán végrehajtott négyzetreemelés iterációs eljárása szintén érdekes szerkezetek megjelenéséhez vezet. Ezek nem geometriai, hanem kombinatorikai szerkezetek. Válasszunk ki véletlenszerűen egy számot 0 és 99 között. Emeljük négyzetre ezt a számot és az eredményből vegyük el az utolsó két számjegyet, melynek szintén egy 0 és 99 közé eső számnak kell lennie.
Például 59²=3481; az utolsó két számjegy a 81. Ismételjük meg az eljárást, és előbb vagy utóbb egy olyan számot fogunk előállítani, amellyel már találkoztunk. A 81 például a 61, 21, 41 és 81 sorhoz vezet, s ennek a négy számnak a sorozata azután végtelenül ismétlődik. Kiderül, hogy az ilyen ciklusok mindig véges halmazokon való iterációs eljárások eredményei. Valóban könnyen belátható, hogy 100 számból álló sorozat esetén 100 művelet elvégzése után legalábbis egy ismétlődő számnak kell lennie; az első ismétlődő szám azután ciklushoz vezet. Van egy csinos kis program, amely érzékeli a ciklusokat, és jóformán nem is igényel memóriakapacitást, de erről majd később.
Csak egyetlen órát vesz igénybe, hogy a négyzetre emelési eljárás eredményét diagramban ábrázoljuk. Ábrázolja egy lapon a 0 és 99 közé eső számokat egy-egy különálló pont. Ha a négyzetre emelési eljárás egy számból új számot eredményez, a meg felelő pontokat nyíllal kössük össze. Például nyílnak kell mutatnia az 59-es számból kiindulva a 81-eshez. A diagramban az első néhány pont összekötése zavaros ciklust eredményezhet, ezért jó ötletnek tűnik időről-időre történő újrarajzolásuk oly módon, hogy két nyíl ne keresztezze egymást. A metszésmentes iterációs diagram megrajzolására mindig van lehetőség.
Még tovább is mehetünk. Gyakran keletkeznek külön aldiagramok, s ezek megjeleníthetők úgy, hogy az iterációból származó szimmetriák némelyikét hangsúlyozzuk. Például a 0 és 99 közé eső egész számok négyzetre emelésének metszésmentes iterációs diagramja hat egymáshoz nem csatlakozó aldiagramot tartalmaz. Az egyes részek azonos párokban fordulnak elő, és minden rész szimmetrikus . Meg tudjuk-e magyarázni ezt a szimmetriát? Mi történne akkor, ha az előző számok helyett a 0 és 119 közé eső egész számokat használnánk? Van-e valamilyen kapcsolat a diagramban talált egymáshoz csatlakozó ábrák és a sorozatban előforduló legnagyobb egész szám között?
Hasonló iterációs minták fordulnak elő a Mandelbrot-halmaz komplex számainak némelyikénél is: c bizonyos értékeire a z²+c kifejezés ismételt iterációját elvégezve a művelet komplex számok véges ciklusának kialakulását eredményezi. A 0+1i komplex szám iterációja például a -1+1i és a 0-1i komplex számok közötti határozatlan ingadozáshoz vezet. A ciklusnak mindössze egyetlen eleme is lehet. Az ilyen ciklusokat, akár véges halmazban találtuk őket, akár a végtelen Mandelbrot-halmazban, attraktoroknak nevezzük.
A 0 és 99 közé eső számok iterációs diagramjának mind a hat része egy attraktort tartalmaz. Az attraktor geometriailag sokszögként reprezentálható, s az azt eredményező számok csoportja faként ábrázolható.
Az attraktorok számítógépes keresésének egy módja az, hogy az újonnan előállított számokat egy erre a célra kijelölt tömbben tároljuk. Az új számot összehasonlítjuk a korábban a tömbben tárolt öszszes számmal. Amennyiben találtunk egy párt, a tömbben az összeillő szám és az újonnan előállított szám között álló összes számot kinyomtatjuk. A módszer egyszerű és könnyedén programozható. A futás azonban hosszú időt vehet igénybe, ha a tömb nagy. Az n számot tartalmazó tömbön belüli attraktorciklusnál az n² nagyságrendű összehasonlítást végzünk el az attraktor feltárásához: minden új számot maximálisan a t tömb n számával kell öszszehasonlítani.
Van egy ügyes kis program, amely sokkal gyorsabban megtalálja az attraktort. A program nem igényel n számú memóriahelyet, hanem csak kettőt, s ez a program a legegyszerűbb programozható zsebszámológépen is programozható. A program Dean Hoffman (Auburn Egyetem) és Lee Mohler (Alabama Egyetem) "Mathematical Recreations for the Programmable Calculator" című, figyelemre méltó könyvében található meg. Nem szükséges mondani, hogy a könyv témái közül jónéhány könnyen adaptálható számítógépprogramokra is.
A program neve RHOP, minthogy a számsorozat, amely végül önmagát ismétli, egy darab kötélhez hasonlít, amelynek az egyik végén hurok van. A sorozat a görög ró betűhöz is hasonlatos. (A program neve a rope, kötél szóból és a görög ró betűből alkotott szójáték.) Két változó van a programban, a slow (lassú) és a fast (gyors). Indításkor mindkét változónak a kezdő szám értékét adjuk. A program iteratív ciklusa csupán három utasítást foglal magában:
                       fast <-- fast*fast (modulo 100)
                       fast <-- fast*fast (modulo 100)
                       slow <-- slow*slow (modulo 100)
A "modulo 100" művelet választja le az eredményből az utolsó két számjegyet. Figyeljük meg, hogy a négyzetre emelést a fast változóra kétszer, a slow változóra viszont csak egyszer végeztük el. A fast változó a ró farkától a fejéig kétszer olyan gyorsan teszi meg az utat, mint a slow. A ró fejrészében a fast utoléri a slow-t, mely idő alatt a slow az út felét tette meg. A program akkor lép ki az iteratív ciklusból, amikor a fast változó egyenlő a slow-val.
Az attraktort úgy azonosítjuk, hogy a slow aktuális értékére újra elvégezzük a négyzetre emelés iterációs folyamatát. Ha ez a szám visszatér, a program megáll és kinyomtatja a közbenső számsorozatot.
Nagy örömömre szolgálna, ha láthatnám az olvasók azon diagramjait, amelyek az iteratív négyzetre emelés hatásait változó méretű véges területeken vizsgálják. A diagramok kézzel vagy számítógéppel is elkészíthetők. A diszkrét iteráció a matematikának manapság kifejlődő, számítógéptudományi, biomatematikai, fizikai és szociológiai alkalmazásokkal bővülő területe. Az elméleti szakemberek érdeklődéssel várhatják Francois Robertnek (Grenoble-i Egyetem) a témakörre vonatkozó könyvét.